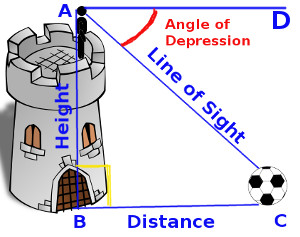
Angle of Depression Examples. If the vehicle is away from the building at a distance of 1meters , find the height of the tower. Solution: In the above figure, R is a vehicle.
PQ is the height of the tower. RQ is the distance between the tower and the vehicle. PS is the line of sight.

So, angle of depression from point B is 45°. BX is the horizontal. Now, we need to find the distance of point A from the building. Now, lines BX and AC are parallel, and AB is the transversal. So, Alternate angles are equal.
The opposite side in this case is usually the height of the observer or height in terms of location, for. Tangent is the main ratio that is used to determine the angle of depression. It may be found by using this equation tan y is equal to opposite divided by the adjacent side.

Problem : From the top of a rock √ m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock. For example, if you were standing on top of a hill or a building, looking down at an object, you could measure the angle of depression. The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object.
You can measure these angles using a clinometer or a theodolite. What is the formula for elevation? How do you calculate angle of depression? What are angles of elevation and depression? Well basically, if your looking at something diagonally above you, you form a sight line.
The angle that would form if it was a real line to the ground is an angle of elevation. How to solve word problems that involve angle of elevation or depression ? Step 1: Draw a sketch of the situation. Step 2: Mark in the given angle of elevation or depression.
Step 3: Use trigonometry to find the required missing length. Example: Two poles on horizontal ground are m apart. To avoid this, cancel and sign in to on your computer.
A pilot is flying over a straight highway.
He determines the angles of depression to two mileposts, 4. Find distance using right triangles and angles of elevation or depression. Click Create Assignment to assign this modality to your LMS. Learn what the terms angle of elevation and angle of depression mean. The words may be big but their meaning is pretty basic! Mathematical problems that require the use of trig functions often have one of two related angles : the angle of elevation or the angle of depression.
The scenarios that use these angles usually involve calculating distances that can’t be physically measured. Animals and artists, pilots and pelicans all instinctively use the angle of depression. From a park ranger in a fire tower to that pilot taxiing or landing an A3airliner, the angle of depression provides important information about distance and height.
Remember that one side of the angle of depression (and also the angle of elevation) is always horizontal. The other side is formed by the line of sight. Let x = distance between stadium and tennis court. Consider right triangle BST. From a police helicopter flying at 3ft, a stolen car is sighted at an angle of depression of 74.
Through the law of alternate angle , it may be seen that the angle of depression and elevation are apparently found to be equal in magnitude, which means α = β. Further, it can be found that Tan α is equivalent to ratio of the height and distance.